Research interests and activities

My research interests and activities can roughly be grouped into these topics; for guidance, I am taking inspiration from research into human learning, especially developmental learning during infancy.

Scalable incremental/continual learning
High-dimensional data description by Deep Gaussian Mixture Models
Object detection in context

Scalable incremental learning

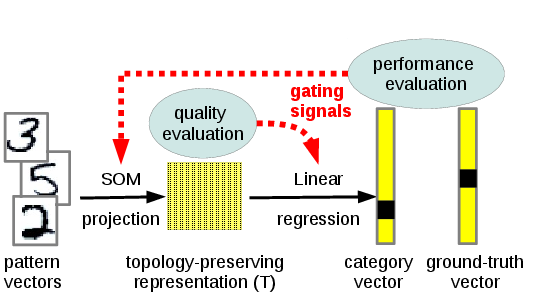
This activity aims at learning algorithms that can learn continuously, without forgetting previously acquired knowledge. In particular, such continual learning algorithms should be

efficient for problems of very high dimensionality (>1000)
scalable, with constant time complexity w.r.t. already learned knowledge
at least partially generative

The focus on generative algorithms is easily explained as in real applications it is imperative to detect outliers, which generative methods are capable of doing, but discriminative ones are not. A particular focus of my recent work is on constant time complexity: in practice, learning performance must not depend on the amount of knowledge that was acquired in the past, since this can be enormous when learning over long time periods. My basic intuition is that a new learning task should only modify similar knowledge already in the system. The challenge is then to devise learning algorithms capable of efficiently querying for this kind of information. Which is what I am currently doing.

Go to top of page

Deep Convolutional Gaussian Mixture Models

This endeavor is related to my research on continual learning, which must, to my mind, necessarily contain an element of replay. However, the standard way of achieving this through GANs has its problems, which stems from the fact that GANs do not have an associated loss function, so there is no way to know whether a GAN is currently undergoing mode collapse, a frequent problem. Replacing GANs by GMMs as generators would be the ideal solution; however the quality of sampling from vanilla GMMs is strongly inferior to GANs. Therefore, I am looking for ways to create stacked convolutional variants of GMMs that can leverage the inherent compositionality if natural images by a hierarchical structure with local receptive fields, analogous to CNNs. Extension of GMMs that allow better sampling behavior, like Mixtures of Factor Analyzers (MFA), are also under investigation.
A first prominent result of these activities is an SGD-based training algorithm for GMMs that works for lage sets of natural images and it superior, both in performance and manageability, to sEM, a stochastic version of EM, the usual training algorithm for GMMs.

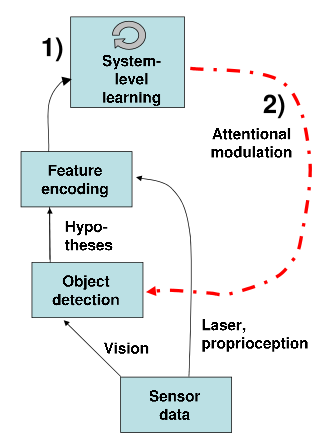
Object detection in context

This line of research aims at learning high-level knowledge such as "pedestrians are usually found on sidewalks and not on roofs", and translating it into lower-level descriptions that can be used to guide local pattern-based detection methods. Not only can such approaches increase the detection accuracy significantly, but also the design time is strongly reduced. I have already suceeded in showing this in the context of vehicle detection, see the paper. I believe this kind of "common sense models" (I term them "context models") that humans have learned for more or less all types of objects in different situations, and the ability to translate them into precise and efficient search strategies, is what makes human perception so powerful.
What interests me currently is the question of how to learn situation-specific context models. As a very obvious example, consider the search for pedestrians in inner-city and highway traffic: while in the former case one might have to look preferentially at the sidewalk, while in the latter case one does not look for pedestrians at all since they are rarely encountered on highways. Recently, I have studied how Gaussian Mixture Models(GMMs) can be used to learn this kind of correlation in an autonomous fashion.

Go to top of page